Relative representations enable zero-shot latent space communication
Abstract
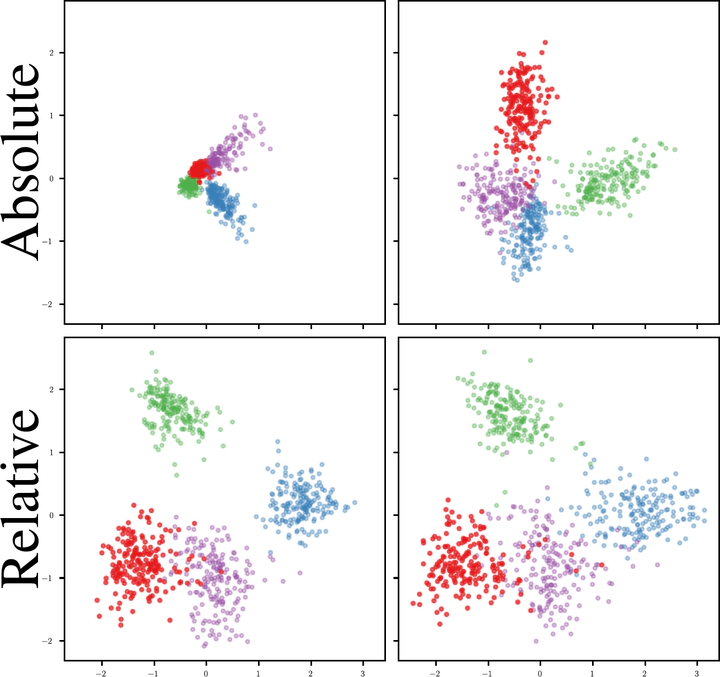
Neural networks embed the geometric structure of a data manifold lying in a high-dimensional space into latent representations. Ideally, the distribution of the data points in the latent space should depend only on the task, the data, the loss, and other architecture-specific constraints. However, factors such as the random weights initialization, training hyperparameters, or other sources of randomness in the training phase may induce incoherent latent spaces that hinder any form of reuse. Nevertheless, we empirically observe that, under the same data and modeling choices, distinct latent spaces typically differ by an unknown quasi-isometric transformation: that is, in each space, the distances between the encodings do not change. In this work, we propose to adopt pairwise similarities as an alternative data representation, that can be used to enforce the desired invariance without any additional training. We show how neural architectures can leverage these relative representations to guarantee, in practice, latent isometry invariance, effectively enabling latent space communication: from zero-shot model stitching to latent space comparison between diverse settings. We extensively validate the generalization capability of our approach on different datasets, spanning various modalities (images, text, graphs), tasks (e.g., classification, reconstruction) and architectures (e.g., CNNs, GCNs, transformers).
Marco Fumero
PhD Student
Antonio Norelli
Alumni
PhD student in AI @ Sapienza University of Rome, CS dep. I love teaching, especially to machines.
