Abstract
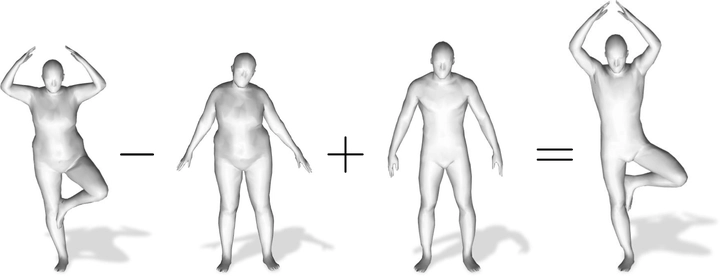
In this paper, we advocate the adoption of metric preservation as a powerful prior for learning latent representations of deformable 3D shapes. Key to our construction is the introduction of a geometric distortion criterion, defined directly on the decoded shapes, translating the preservation of the metric on the decoding to the formation of linear paths in the underlying latent space. Our rationale lies in the observation that training samples alone are often insufficient to endow generative models with high fidelity, motivating the need for large training datasets. In contrast, metric preservation provides a rigorous way to control the amount of geometric distortion incurring in the construction of the latent space, leading in turn to synthetic samples of higher quality. We further demonstrate, for the first time, the adoption of differentiable intrinsic distances in the backpropagation of a geodesic loss. Our geometric priors are particularly relevant in the presence of scarce training data, where learning any meaningful latent structure can be especially challenging. The effectiveness and potential of our generative model is showcased in applications of style transfer, content generation, and shape completion.
Luca Cosmo
Assistant Professor
Antonio Norelli
Alumni
PhD student in AI @ Sapienza University of Rome, CS dep. I love teaching, especially to machines.
