Abstract
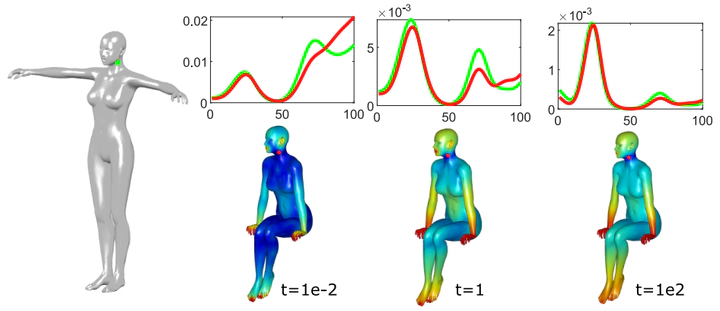
We introduce the Average Mixing Kernel Signature (AMKS), a novel signature for points on non-rigid three-dimensional shapes based on the average mixing kernel and continuous-time quantum walks. The average mixing kernel holds information on the average transition probabilities of a quantum walk between each pair of vertices of the mesh until a time T. We define the AMKS by decomposing the spectral contributions of the kernel into several bands, allowing us to limit the influence of noise-dominated high-frequency components and obtain a more descriptive signature. We also show through a perturbation theory analysis of the kernel that choosing a finite stopping time T leads to noise and deformation robustness for the AMKS. We perform an extensive experimental evaluation on two widely used shape matching datasets under varying level of noise, showing that the AMKS outperforms two state-of-the-art descriptors, namely the Heat Kernel Signature (HKS) and the similarly quantum-walk based Wave Kernel Signature (WKS).