Abstract
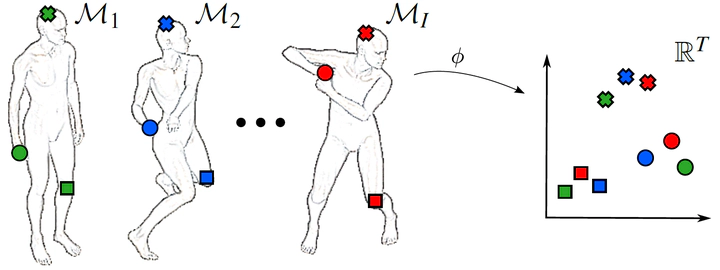
We propose novel point descriptors for 3D shapes with the potential to match two shapes of the same object under natural deformations. These deformations are more general than the often assumed isometries, and we use labeled training data to learn optimal descriptors for such cases. Furthermore, instead of explicitly defining the descriptor, we introduce new Mercer kernels, for which we formally show that their corresponding feature space mapping is a generalization of either the Heat Kernel Signature or the Wave Kernel Signature. We show that the proposed descriptors are guaranteed to be at least as precise as any Heat Kernel Signature or Wave Kernel Signature of any parameterization. In experiments, we show that our implicitly defined, infinite-dimensional descriptors can better deal with slightly non-isometric deformations than state-of-the-art methods.