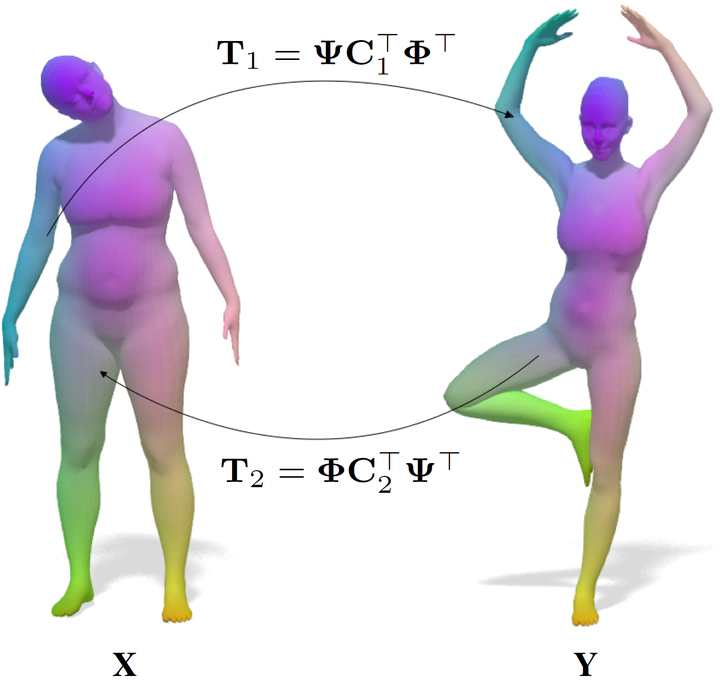
Abstract
Classical formulations of the shape matching problem involve the definition of a matching cost that directly depends on the action of the desired map when applied to some input data. Such formulations are typically one-sided - they seek for a mapping from one shape to the other, but not vice versa. In this paper we consider an unbiased formulation of this problem, in which we solve simultaneously for a low-distortion map relating the two given shapes and its inverse. We phrase the problem in the spectral domain using the language of functional maps, resulting in an especially compact and efficient optimization problem. The benefits of our proposed regularization are especially evident in the scarce data setting, where we demonstrate highly competitive results with respect to the state of the art.