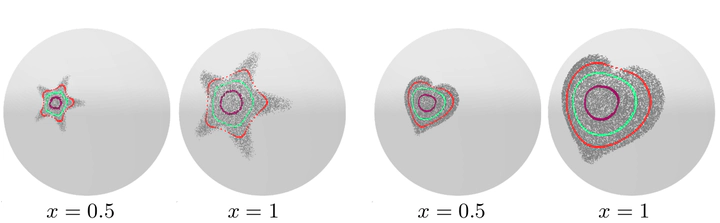
Abstract
Quantile regression (QR) is a statistical tool for distribution-free estimation of conditional quantiles of a target variable given explanatory features. QR is limited by the assumption that the target distribution is univariate and defined on an Euclidean domain. Although the notion of quantiles was recently extended to multi-variate distributions, QR for multi-variate distributions on manifolds remains underexplored, even though many important applications inherently involve data distributed on, e.g., spheres (climate measurements), tori (dihedral angles in proteins), or Lie groups (attitude in navigation). By leveraging optimal transport theory and the notion of $c$-concave functions, we meaningfully define conditional vector quantile functions of high-dimensional variables on manifolds (M-CVQFs). Our approach allows for quantile estimation, regression, and computation of conditional confidence sets. We demonstrate the approach’s efficacy and provide insights regarding the meaning of non-Euclidean quantiles through preliminary synthetic data experiments.
Marco Pegoraro
PhD Student
I am a Ph.D. student in Geometric Deep Learning. My research activity is focused on spectral geometry processing applied to graph learning and computational biology.
Irene Tallini
PhD Student
I’m a Computer Science PhD with Math Bachelor and passion. Right now I’m working on AI for Music. I like to sing, also.
