Abstract
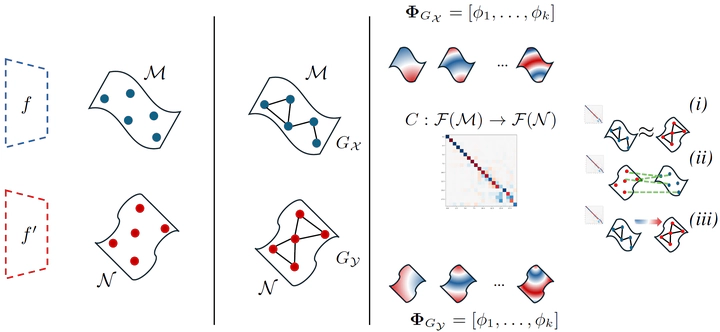
Neural models learn data representations that lie on low-dimensional manifolds, yet modeling the relation between these representational spaces is an ongoing challenge. By integrating spectral geometry principles into neural modeling, we show that this problem can be better addressed in the functional domain, mitigating complexity, while enhancing interpretability and performances on downstream tasks. To this end, we introduce a multi-purpose framework to the representation learning community, which allows to: (i) compare different spaces in an interpretable way and measure their intrinsic similarity; (ii) find correspondences between them, both in unsupervised and weakly supervised settings, and (iii) to effectively transfer representations between distinct spaces. We validate our framework on various applications, ranging from stitching to retrieval tasks, demonstrating that latent functional maps can serve as a swiss-army knife for representation alignment.
Marco Fumero
PhD Student
Marco Pegoraro
PhD Student
I am a Ph.D. student in Geometric Deep Learning. My research activity is focused on spectral geometry processing applied to graph learning and computational biology.
